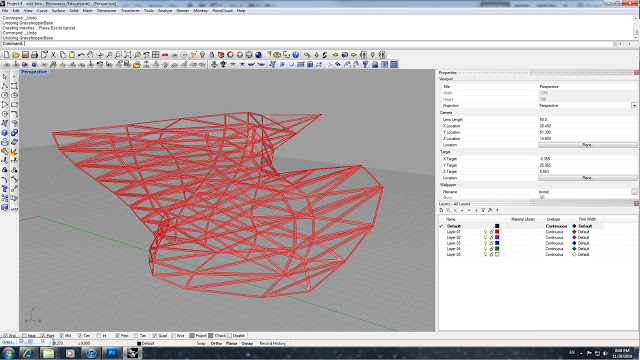
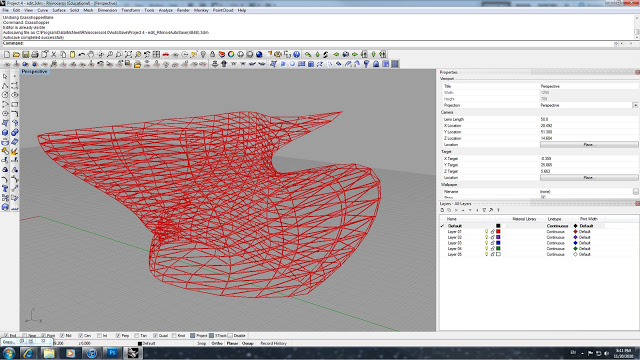
This project was an assignment to create a parametric truss system and have it spanning along a large surface. I was also interested in seeing how it would perform on a complex/irregular/non-uniform single surface.
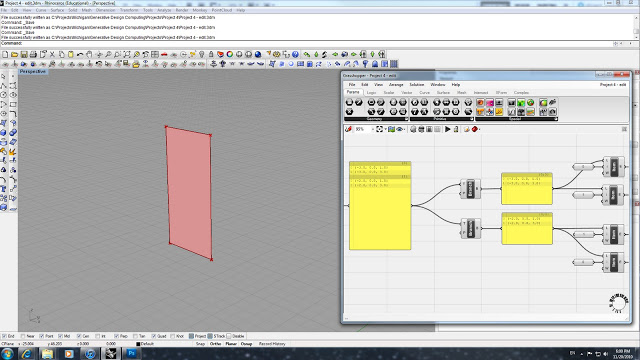
The first step is to begin building a basic truss on a rectangular surface. First we set a Surface function and attach that to a Surface Divide function. In order to get 4 corner points, we set the SDivide function's U and V value at 1. We then attach a Simplify function along with a notepad to confirm that we have correctly setup the points, and into 2 different categories.
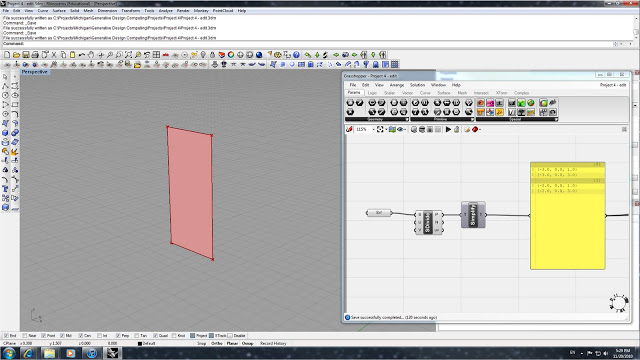

The next step is set up 2 different branches which will separate the points into 2 groups. The top Branch is set to receive the points from category 0, while the bottom Branch will receive points from category 1 - this is achieved by setting P to 0 for the top and 1 for the bottom Branch. The branches are further broken down into single points by using the Item functions and setting the integer (i) values to 0 and 1 for each of the two branches.
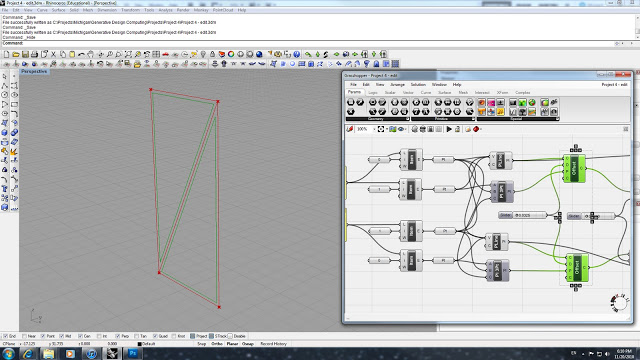
Once the individual items were set, we assign a single Point to each Item. The next step was to create a solid polyline and a plane using 3 points. By using the PLine function, we attach 3 points to create the closed polyline and the Plane 3pt function determines the plane that the polyline lies on. All of the these functions are done twice to create 2 different triangles that bisect the rectangular surface. Once the polylines are created, we can offset them by using the Offset function, attaching the polylines as the input curves and using the Plane 3pt as the plane in which to offset. By attaching a slider we are able to control the distance of the offset, and if the offset is in the wrong direction we can set a -d expression to reverse the offset side.
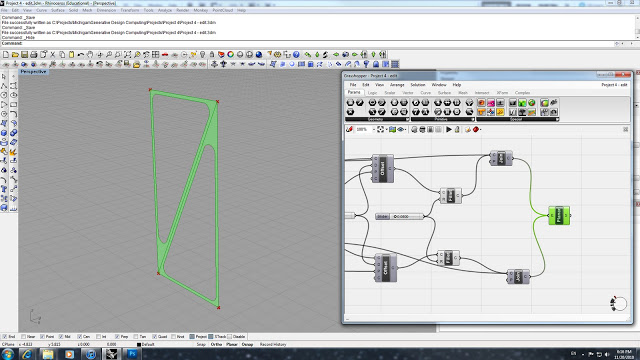
The last step with the single surface truss is to set a Fillet function with a slider to adjust the fillet radius. We then attach this polyline with the original perimeter triangle geometry into a Join function. The final step is to assign a Planar function to create surface between the perimeter trinagle and the offset polyline.
The second half of this tutorial is to show the steps of how to assign the single surface truss onto a large and comnplex surface. After creating the complex surface, we assign it to a Surface parameter and plug that into a Divide and into a SubSrf (Isotrim) function. The Divide function has numeric sliders to control the amounts of divisions in the U and V directions. This is then plugged into a SDivide function to add points at the corners - the U and V values must be set to 1 to achieve this. Finally a Simplify function is added to eliminate overlapped/redundant points.
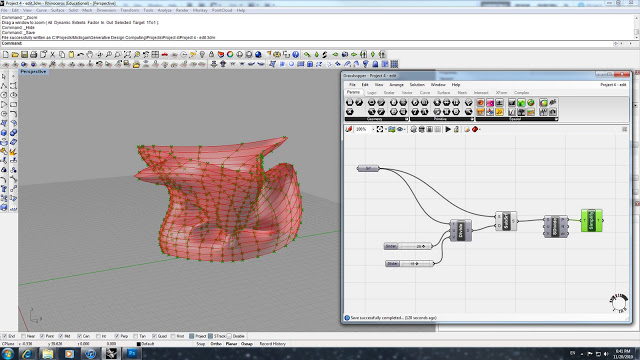
Now we use this new surface and all of its divisions and replace the original single surface and the components - everything up to the first, original notepad.
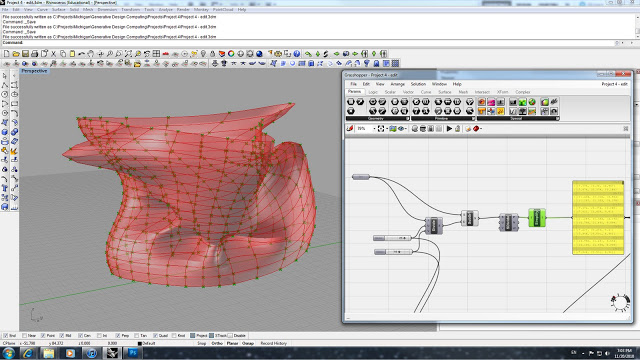
The next step is to use a Param Viewer function in order to take the detailed information and translating this into individual paths - info from the first notepad is the input data for the Param Viewer. We use a notepad to see the list of the newly translated individual paths, and then plug these into two different Item functions. The Item functions are then plugged back into the original Branch path slots (P).
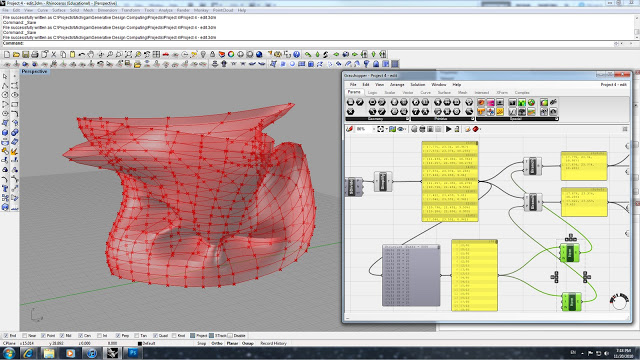
The final step is to insert a Series and Multiply function and to insert the surface's division sliders into the Multiply function. This will all for an accurate number of individual trusses to be applied to the U and V subsurfaces that have been created by the division. The Multiply function is plugged into the Series, and the Series is then plugged into both of the Item functions.
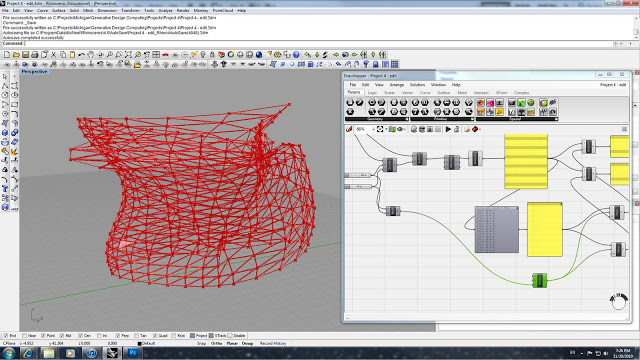
This is the final output geometry with 10x10 divisions and an offset of 1.1.
This is the final output geometry with 22x22 divisions and an offset of .02.